As discussed in an excellent Education Datalab post (here), the government is judging schools using Progress metrics which are strongly related to schools’ average intake attainment and have a large grammar school ‘effect’. As the article’s author, Dr (now Professor) Rebecca Allen notes, ‘The problem is that we don’t know why.’
My most recent research provides an answer. Namely, that this effect is almost entirely down to a measurement bias (rather than genuine differences in school effectiveness).
I wrote an ‘Expert Piece’ in Schools Week about this to try and get the message out. Understandably, my word limit was tight and diagrams or any semi-technical terms were not permitted. So this blog fills in the gap between the full research paper (also available here) and my Schools Week opinion piece, providing an accessible summary of what the problem is and why you should care.
The Ability Bias and Grammar School Effect
Take a look at the relationship between Progress 8 and average KS2 APS in the 2017 (final) secondary school scores:
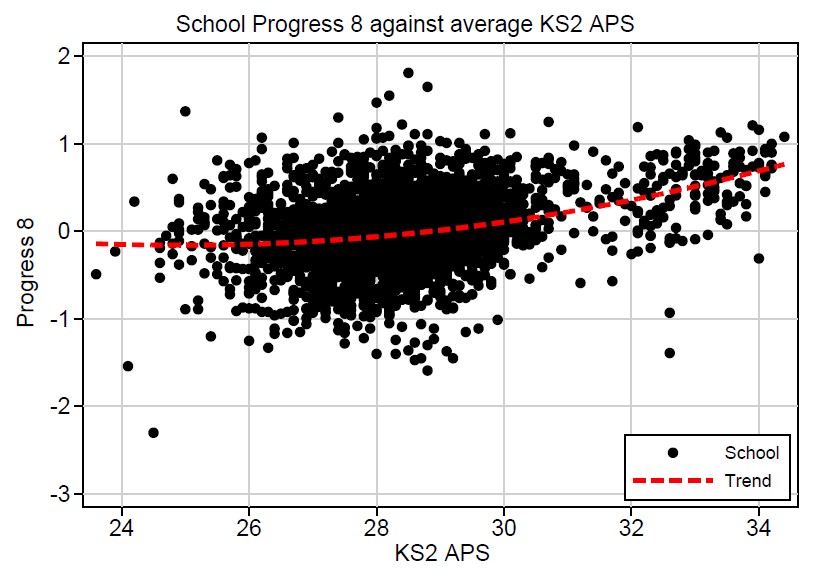
One hardly needs the trend line to see an upwards pointing arrow in the school data points. As one moves to the right (average KS2 APS is higher), Progress 8 tends to increase. As Education Datalab’s Dave Thomson points out, likely explanations include (I quote):
- Their pupils tend to differ from other pupils with similar prior attainment in ways that have an effect on Key Stage 4 outcomes. They may tend to receive more support at home, for example;
- Their pupils have an effect on each other. Competition between pupils may be driving up their performance. There may be more time for teaching and learning due to pupils creating a more ordered environment for teaching and learning through better behaviour; or
- They may actually be more effective. They may be able to recruit better teachers, for example, because they tend to be the type of school the best teachers want to work.
There is one explanation missing from this list: namely, measurement error prevents the Progress scores fully correcting for intake ability and biases remain in the school-level scores.
In my paper I conclude that this is the most likely explanation and measurement error alone produces bias remarkably similar to that seen in the graph above. To find out why, read on:
What causes this bias?
Technical Explanation:
A technical answer is that this the observed peer ability effect is caused by a so-called ‘Phantom’ compositional effect produced by regression attenuation bias (NB. For stats nerds, I realise the Progress scores are not produced using regressions and discuss in the paper how ‘attenuation bias is not a peculiarity of certain regression equations or value-added models and will also affect the English ‘Progress’ scores’. Also see non-technical explanation below).
Non-technical Explanation (based on my Schools Week piece):
Put very simply, if we have imperfect measures of prior attainment, we will get an incomplete correction for ability. We will end up with some middle ground between the original KS4 scores – which are strongly correlated with intake prior attainment – and a perfect school value-added score for which intake ability doesn’t matter.
The problem is caused by two issues:
Issue 1: Shrinking expectations (technically, regression attenuation bias)
Progress 8 expectations rely on the relationship between KS2 and KS4 scores. As error increases, this relationship breaks down as pupils of different ability levels get mixed up. Imagine that the KS2 scores were so riddled with error that didn’t predict KS4 scores at all. In this scenario, our best expectation would be the national average. At the other extreme, imagine a perfect KS2 measure. Our expectations would be perfectly tailored to all pupils’ actual ability levels. With normal levels of error, we end up at an interim position between these where the relationship moderately breaks down and the expectations shrink a little to the national average (and consider what happens to the value-added as they do).
If you are interested in exactly what causes this – I have written a short explanation here (with a handy diagram).
Issue 2: ‘Phantom’ effects
Up until now, the conventional wisdom was that there is going to be some level of unreliability in the test scores, but much of this would cancel out in the school averages (some students get lucky, others unlucky, but it evens out as cohorts get larger) and tests were designed to avoid systematic biases (although of course this is contested). So there was no reason to think that random error could produce systematic bias.
It turns out this is wrong. Here’s why:
The second issue here is that of ‘Phantom’ effects, where measurement error creates relationships between school average scores (e.g. between KS2 and KS4 school scores) despite the relationship being corrected using the pupil scores. Researchers have known about this for some time and have been wrestling with how to measure the effect of school composition (e.g. average ability) without falling for phantoms.
A big conceptual barrier for thinking clearly about this is that relationships and numbers can behave very differently depending whether you are using averages or individual scores. The English Progress measures use individual pupil Key Stage scores. School averages are created afterwards. The data points on the Education Datalab graph mentioned above (here) are all school averages.
The designers of the Progress measures did a great job of eliminating all observable bias in the pupil scores. They had their hands tied however when designing the measures (see p.6 here) when it came to correcting anything else. When we work out the school averages, the relationship between KS2 and KS4 pops up again – a ‘phantom’ effect!
Why does this happen? If a gremlin added lots of random errors to your pupil’s KS2 scores overnight, this would play havok with any pupil targets/expectations based on KS2 scores, but it might have little effect on your school average KS2 score. The handy thing about averages is that a lot of the pupil errors cancel out.
This applies to relationships as well. It is not just the school average scores which hold remarkably firm as we introduce errors into pupil scores, it is the relationships between them. As we introduce errors into the pupils’ scores – due to errors cancelling out – each school’s average would be left largely unaffected – leaving the relationship between school average KS2 and KS4 intact.
In other words, as measurement error is increased, a relationship will break down more in the pupil scores than for school averages. This means that to some extent, the school level KS2-KS4 relationship will be what left over from an incomplete correction of the pupil scores and an apparent (phantom) ‘compositional’ effect pops up. In the words of Harker And Tymms (2004) – the school averages ‘mop-up’ the relationship obscured by error at the pupil-level.
The Progress 8 measures only correct for pupil scores. They do not take school averages into account. If there is KS2 measures error – which there will be (especially judging it be recent years events!) – the correction at pupil level will inevitably be incomplete. The school averages will therefore mop this up, resulting in an ability bias.
Okay, so that’s the theory. Does this matter in practice?
This effect is inevitable to some extent. But it might not be serious. The big question I set out to answer in my research paper was how big the bias will be in the English Progress measures for typical rates of KS2 measurement error.
I used reliability estimates based on Ofqual research and ran simulations using the National Pupil Database. I used several levels of measurement error which I labelled small, medium and large (where the medium was the best estimate based on Ofqual data).
I found that KS2 measurement error produces a serious ability bias, complete with a ‘phantom grammar school effect’. For the ‘medium’ error, the ability bias and the (completely spurious) grammar school effect were remarkably similar to the one seen in the actual data (as shown in the graph above).
I also looked at the grammar school effect in DfE data from 2004-2016, finding that it lurched about from year to year and with changes in the value-added measure (to CVA and back) and underlying assessments.
What should we do about this?
There is a quick and easy fix for this: correct for the school-level relationship, as shown visually in the aforementioned Education Datalab post. (There are also so more technical fixes involving estimating baseline measurement reliability and then correcting for it in the statistical models). Using the quick-fix method, I estimate in my paper that about 90% of the bias can be removed by adjusting for school average prior attainment.
Here’s what that would look like (using final 2017 data):
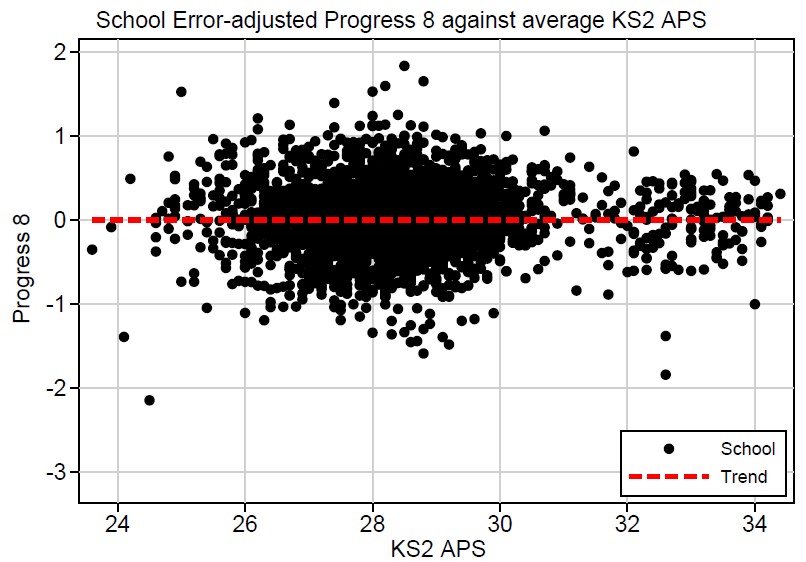
While this is technically easy to do, there are enormous political and practical ramifications of making a correction which would substantially shift all Progress scores – primary and secondary – across the board and would eliminate the grammar school effect entirely. Schools with particularly low or high ability intakes, grammar schools especially, will find themselves with a markedly different Progress scores. This might prove controversial…
But it is in keeping with the clear principle behind the Progress measures: schools should be judged by the progress their pupils make rather than the starting points of their pupils. We just need to add that schools should not be advantaged or disadvantaged by the average prior attainment of their intake any more than that of individual pupils.
There is a whole other argument about other differences in intakes (so-called contextual factors). Other researchers and I have examined the (substantial) impact on the school scores of ignoring contextual factors (e.g. here) and there is strong general agreement amongst researchers that contextual factors matter and have predictable and significant effects on pupil performance.
Here the issue is more fundamental: by only taking pupil-level prior attainment scores into account, the current Progress measures do not even level the playing field in terms of prior attainment (!)
Links and References
- See my the Schools Week article here
- The article will be in print shortly and is currently available online for those with university library logons and, for those without university library access, the accepted manuscript is here
- I have also produced a 1-page summary here
I have not provided citations/references within this blog post but – as detailed in my paper – my study builds on and is informed by many other researchers to whom I am very grateful. Full references can be found on my journal paper (see link above).

Could you calculate Grammar school averages if this was corrected so that we could see the difference
LikeLike
It depends how it was corrected. The currently observed grammar school effect is a consequence of a) measurement error (and the problem I am highlighting) and b) any differences in grammar school performance – positive or negative – relative to other schools. My view is that is is mostly the former and we can just correct this by taking out both (as in the final scatter plot above). But this would rule out any potential grammar school effect; in effect, it would just compare grammar schools to each other. The slightly more challenging option is to reach an estimate of measurement error in KS2 scores. We could then adjust for this and potentially leave b. But I think we are not in the position where KS2 measurement error and its characteristics are entirely clear and I am not confident that what was left over could be taken as a measure of grammar school performance (i.e. b). In short, I think comparing schools of different types and intake is problematic, we don’t really know how to do it and it probably isn’t a valuable thing to be trying to do anyway – nonetheless, leaving clear and substantial biases towards different schools in this was is unhelpful and unnecessary as it is easily fixed.
LikeLike